7自由度冗長マニピュレータの機構解析

原子力基盤技術データベースのメインページへ
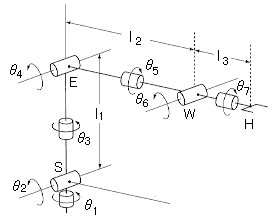
作成： 2000/03/15 佐々木　忍データ番号　　　：120042 7自由度冗長マニピュレータの機構解析目的　　　　　　：7自由度冗長マニピュレータに対するアーム解の効率的な誘導方法の開発研究実施機関名　：日本原子力研究所東海研究所中性子科学研究センター応用分野　　　　：ロボット・マニピュレータの位置・姿勢制御,特異点の解析,特異点の回避,障害物の回避概要　　　　　　：　冗長性をもつ腕機構は、特異点の回避や障害物との衝突回避等に役立つ反面、解を誘導する取扱いが困難なことから、特に球面状関節の手首をもつ7自由度機構に対して、アーム平面と基準平面の角度、すなわち人間の肘の旋回角をパラメータとして各関節角の単純な解析表現を与えた。さらに、速度ヤコビアンを通して、座標変換や原点移動、関節軸の平行・直交性等を考慮に入れた簡略化により関節角速度の閉形式表現を導いた。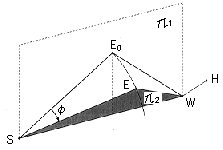　詳細説明　　　　：図1　Schematic of seven-joint manipulator 図2　Definition of elbow angle φ 　図1に記載したマニピュレータは、肩(S)、肘(E)、手首(W)、ハンド(H)から構成される人間の腕を模擬した7関節形冗長機構である。逆問題の解法の概要を述べるために、図2に示すような指定位置にあるハンドに対して、手首、肘、肩を含む一つの平面を考える。まず、3関節軸が直交する球面状関節の手首に対して、WH間軸方向単位ベクトルを基準座標系Σ₀へ射影した方向余弦を使って、手首の位置Wが容易に定まる。一方、この手首の位置は視察や簡単な計算でθ₁からθ₄で決定することがわかる。しかしながら、この姿勢を実現する角度θ₁～θ₄は一意的には決らない。つまり、手首の位置を固定しても、肘が肩・手首を結ぶ直線まわりに回転する自由度が残るため腕姿勢が定まらず、図のような肘旋回角φを利用した冗長度の決定が考えられる。　　いま、肘の現在位置E₀がS、Wおよびz軸を含む平面π₁上にあるとすれば、その位置は幾何学的関係の考察から容易に引出せる。このE₀を指定角度φだけ回転する変換操作により肘位置Eが確定すると、最初の関節角θ₁、θ₂またθ₃が順に決定する。もちろん、θ₄は△SE₀Wの外角として余弦法則を使って求められる。　　他方、手首と指先(ハンド)間の姿勢関係A₅A₆A₇ = (A₁A₂A₃A₄)^-¹A_e_q(A_e_qは与えられた指先の位置・姿勢を表わす斉次行列)から、この行列式を整理すると残る関節角θ₅、θ₆、θ₇の解析的な記述がこの順序で得られる。なお、各関節角が与えられた場合の肘旋回角φは、図2に示すようにS、Wおよびz軸を含む基準平面π₁と直線SWのまわりに旋回した肘Eが作る新しい平面π₂の交角として算出できる。　　図1に対する各関節角の閉形式表現に続いて、つぎにその角速度の閉形式表現を取り扱う。ハンド先端の速度υ(並進速度Vと角速度ω)とジョイント速度の関係は速度ヤコビアンと呼ぶ関数行列式で記述され、ベースに固定した基準座標系Σ₀からみたj番目の列は[(^bk_j×^bz_j)^T,(^bk_j)^T]^Tとコンパクトに表現されるものの、実際の取扱いは極めて手間を要す。ただ、この軸ベクトル^bk_jは、座標系Σ_j_-₁のz軸方向単位ベクトルk_jをΣ₀のz方向ベクトルに変換することで比較的容易に算出できる。その際、再帰的表現の利用が効果的で、上の列はj番目の座標系の方向余弦やその位置と先端とのモーメントを扱う計算となり、回転・直動両関節の選択も自由にできる。　　しかしながら、その結果は一般に関節の数が増えると共に煩雑化する傾向をもち、関節の角速度の誘導や特異点解析への適用に対してなお障害になる。そこで、これまでに定着していた基準座標系の概念をベースから作業空間の適当な位置(例えば手首やそれに近い関節)に移動させ、この点を起点にして元のリンク・関節系を見直す方法をとる。一点に関節が集中する動作形態を中心に、個々の関節軸の交差状況を調査することが重要となる。基準座標系を任意の関節iの位置に移して、固定したこの座標系Σ_i_-₁からみたハンドの速度関係を導く。ヤコビアンのj番目の列はΣ_j_-₁とΣ_i_-₁の方向余弦、ハンドとj番目の距離等を含む簡単な四則演算として表わされる。　　特に、関節軸の平行、直交に対応した演算や球面状関節の手首機構等が現在のロボットに対する6×7ヤコビアンの行列要素の一部を零にする等大幅な要素の簡略化を実現し、各ジョイント角速度の解析的表現が可能になる。関節系へのある拘束条件追加した拡張ヤコビアンにより、例えばθ₂+θ₄=C(一定)を仮定した体系での腕の特異点状況等が明らかになる。一連の操作は数式処理ソフトを利用することで逆問題の解析解が自動的に生成される。　コメント　　　　：　冗長マニピュレータの逆問題は、一般化逆行列を始めとしていくつかの数値的反復法が提案されているが、人間の肘の動きに着目した関節解の表現や速度ヤコビアンの変換諸操作を通して誘導されたジョイント角速度の表現は、複雑で柔軟な腕の動きの効率的な決定に役立つばかりか、特異点の回避やその分布状況を明らかにする上で意義がある。　原論文１ Data source 1： Feasibility studies of kinematic problems in the case of a class of redundant manipulators S. Sasaki Tokai Research Establishment, Japan Atomic Energy Researh Institute, Tokai-mura, Naka-gun, Ibaraki-ken 319-1106 Japan Robotica, Volume 13 (1995) pp. 233-241. 参考資料１ Reference 1： R.P. Paul Robot Manipulators; Mathematics Programming and Control, MIT Press (1981). キーワード：7自由度冗長マニピュレータ,人間型腕機構,肘旋回角,逆問題,球面状関節,速度ヤコビアン 7DOF redundant manipulator, anthropomorphic arm mechanism, elbow angle, inverse problems, spherical joint, velocity Jacobian 分類コード：120207
原子力基盤技術データベースのメインページへ